The Long View: Is Mathematics Constitutional?
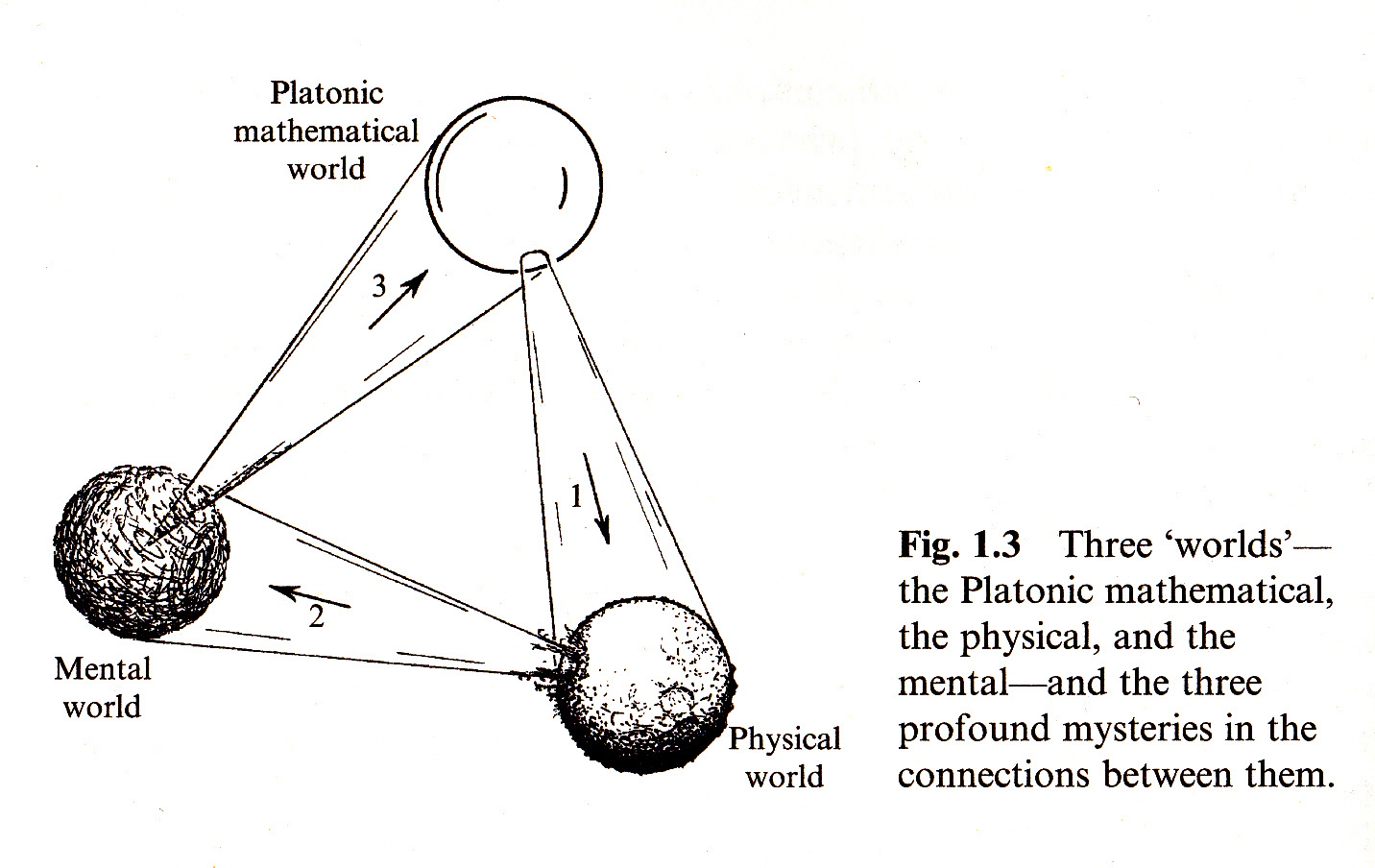
A recent popular [well, as popular as a massive book full of equations can be] exposition of mathematical Platonism is Roger Penrose's The Road to Reality. It even has practice problems in it with devoted communities of amateurs trading tips on how to solve them. Mathematical Platonism, or something much like it, really is something like the default position of many mathematicians and physicists.
Since I ended up an engineer, perhaps it isn't really surprising that I always found the moderate realism of Aristotle and Aquinas more appealing.
There is a good quote in this short essay that I've used to good effect:
"Because the whole point of science is to explain the universe without invoking the supernatural, the failure to explain rationally the 'unreasonable effectiveness of mathematics,' as the physicist Eugene Wigner once put it, is something of a scandal, an enormous gap in human understanding."
I, for one, was a little taken aback by the proposition that science had any "point" other than to describe the physical world as it actually is, but let that pass.
Philosophy of science is a field in fine shape, but many fans of science try to use it as a cudgel upon religious believers. Insofar as that attempt is mostly ignorant of both science and philosophy, it isn't particularly illuminating.
Is Mathematics Constitutional?
The New York Times remains our paper of record, even in matters of metaphysics. For proof, you need only consult the article by George Johnson that appeared in the Science Section on February 16, 1998, entitled: "Useful Invention or Absolute Truth: What Is Math?" The piece was occasioned by a flurry of recent books challenging mathematical Platonism. This is the belief, shared by most mathematicians and many physicists, that mathematical ideas are "discovered" rather than constructed by the mathematicians who articulate them. Consider the following sentence:
"Because the whole point of science is to explain the universe without invoking the supernatural, the failure to explain rationally the 'unreasonable effectiveness of mathematics,' as the physicist Eugene Wigner once put it, is something of a scandal, an enormous gap in human understanding."
I, for one, was a little taken aback by the proposition that science had any "point" other than to describe the physical world as it actually is, but let that pass. The immediate philosophical peril to the world of the Times is more narrow. That is, it is hard to be a thoroughgoing secular materialist if you have to acknowledge that there are aspects of reality that cannot be explained as either products of blind chance or of human invention. Supreme Court Justice William Kennedy has even suggested that systems of ethics claiming an extra-human origin are per se unconstitutional. Judging by some of the arguments against mathematical Platonism presented by the Times piece, however, we may soon see Establishment Clause challenges to federal aid for mathematical education.
The best-known of the books that try to de-Platonize mathematics is "The Number Sense: How the Mind Creates Mathematics," by the cognitive scientist Stanislas Dehaene. His argument is that the rudiments of mathematics are hardwired into the human brain, and so that mathematics is foundationally a product of neurology. The evidence is various. There are studies of accident victims suggesting there may be a specific area of the brain concerned with counting, as well as stimulus-response studies showing that some animals can be trained to distinguish small-number sequences. (Remember the rabbits in "Watership Down," who had the same name for all numbers from five to infinity?) Relying on even more subtle arguments is a recent article by George Lakoff and Rafael E. Núñez, "Mathematical Reasoning: Analogies, Metaphors and Images." [BE: the actual article is titled The Metaphorical Structure of Mathematics: Sketching Out Cognitive Foundations for a Mind-Based Mathematics] The authors suggest that numbers are simply extrapolated from the structure of the body and mathematical operations from movement. (The article is part of an upcoming book to be called "The Mathematical Body.")
I have not read these works, so it is entirely possible I am missing something. Still, it seems to me that there are two major problems with analyses of this sort. First, if the proposition is that mathematical entities are metaphysical universals that are reflected in the physical world, it is no argument against this proposition to point to specific physical instances of them. In other words, if numbers are everywhere, then it stands to reason that they would be inherent in the structure of the brain and body, too.
If Dr. Dehaene has really found a "math-box" in the head, has he found a fantasy-gland or an organ of perception? The Times article paraphrases him as saying that numbers are "artifacts of the way the brain parses the world...like colors. Red apples are not inherently red. They reflect light at wavelengths that the brain...interprets as red." The distinction between things that are "really red" and those that "just look like red" has always escaped me, even in languages with different verbs for adjectival predicates and the copula. Doesn't a perfectly objective spectral signature identify any red object? In order to avoid writing the Monty Python skit that arguments about perception usually become, let me just note here that the experience of qualia (such as "redness") has nothing to do with the cognitive understanding of number. Like the numbers distinguishing the wavelengths of colors, for instance.
There is a more basic objection to the physicalistic reductionism at work here, however. Consider what it would mean if it worked. Suppose that proofs were presented so compelling as to convince any honest person that mathematics was indeed nothing more than an extrapolation of the structure of the nervous system, or of the fingers on the hand, or of the spacing of heartbeats. We would then have a situation where we would have to explain the "unreasonable effectiveness" of the human neocortex, or even the universal explanatory power of the human anatomy. This would be anthropocentrism come home to roost. You could, I suppose, argue that we only imagine that the human neurological activity called mathematics lets us explain everything; the reality is that we only know about the things that our brains let us explain. Well, maybe, but then that suggests that there are other things that we don't know about because our brains are not hardwired to explain them. Maybe those are the things that are really red?
There are indeed problems with mathematical Platonism, the chief of which is that it is hard to see how the physical world could interact with the non-sensuous ideal forms. (John Barrow's delightful "Pi in the Sky" will take interested readers on a fair-minded tour of the philosophy and intellectual history of this perennial question.) The most workable solution is probably the "moderate Realism" of Aquinas. He held that, yes, there are universals, but that we can know about them only through the senses. This seems reasonable enough. In fact, this epistemological optimism is probably the reason science developed in the West in the first place. There may even be a place for Dr. Dehaene's math-box in all this, if its function is regarded as perceiving numbers rather than making them up. What there can be no place for is the bigotry of those who believe that science exists only to support certain metaphysical prejudices.
Copyright © 1998 by John J. Reilly
Comments ()