The Dangers of Correlation and the Necessity of Scatterplots
After my previous post on IQ and Height, I thought it would be good to revisit the subjects of scatterplots and correlation. A scatterplot is often an excellent first step in any data analysis. You can learn a lot from a scatterplot, because humans are good at pattern recognition. A lot of silly analysis could be avoided by looking at a scatterplot. One of my main complaints about the articles I read for the IQ and Height post was that none of them included a scatterplot.
However, they all reported an r or r2 value. Correlation coefficients are particularly dangerous, because there is a hidden assumption in the mathematics. Correlation coefficients seem very simple, but there is an assumption that the data falls along a straight line with only random variation. When there is some other kind of relationship, the correlation coefficient will not let you know. There are purely mathematical ways to check for this, but why bother when you can see it?
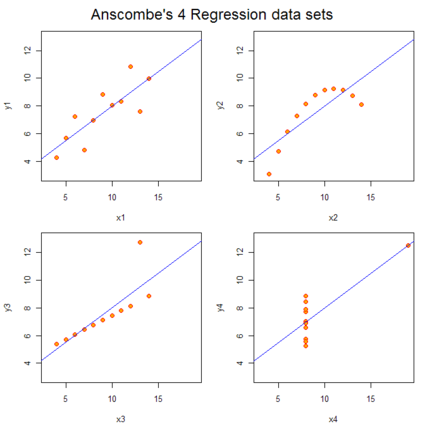
The best illustration of this I have ever seen was published by F. J. Anscombe in The American Statistican in 1973. I have seen this same graph referenced repeatedly in other places, and the data set used to create the graph is even contained in the standard R distribution. If you would like to see the data and graph yourself in R, check out the code.
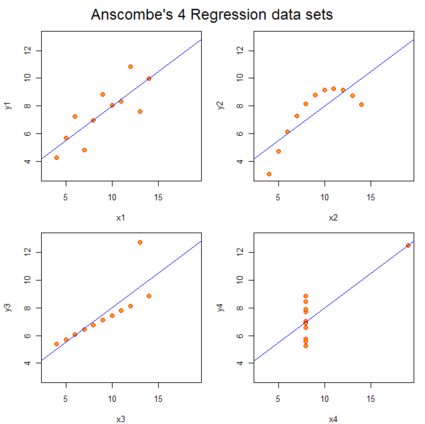
Anscombe's Quartet
Anscombe created these data sets to not only have the same r value, but they also have the same mean and same least-squares fit. For the first three, Anscombe noted that you might not even notice something was amiss if you just ran your eye down the data table, because the data points are not always in order. Hopefully if your data looked like case 4, you would notice.
The moral here is beware of correlations, and graph your data.
Anscombe's Data Sets
| x | y1 | y2 | y3 | x4 | y4 |
| 10 | 8.04 | 9.14 | 7.46 | 8 | 6.58 |
| 8 | 6.95 | 8.14 | 6.77 | 8 | 5.76 |
| 13 | 7.58 | 8.74 | 12.74 | 8 | 7.71 |
| 9 | 8.81 | 8.77 | 7.11 | 8 | 8.84 |
| 11 | 8.33 | 9.26 | 7.81 | 8 | 8.47 |
| 14 | 9.96 | 8.10 | 8.84 | 8 | 7.04 |
| 6 | 7.24 | 6.13 | 6.08 | 8 | 5.25 |
| 4 | 4.26 | 3.10 | 5.39 | 19 | 12.50 |
| 12 | 10.84 | 9.13 | 8.15 | 8 | 5.56 |
| 7 | 4.82 | 7.26 | 6.42 | 8 | 7.91 |
| 5 | 5.68 | 4.74 | 5.73 | 8 | 6.89 |

Comments ()